

More specifically, the' invention relates to an oscillating means being protected from interfering signals so as to provide a truly random sequence of bits when fed by a noise signal. The present'invention relates to a device for generating a random bit sequence.
Moore III, An exhaustive analysis of multiplicative congruential random number generators with modulus 2 31 – 1, SIAM Journal of Scientific and Statistical Computing, Vol. But it’s not enough for many scientific applications. That’s a lot if you’re writing a little game, for example. So our LCG has a period of about two billion values. If the multiplier were not chosen carefully it could have a shorter period. Since the state only depends on the last value, every time it comes to a given output, the next output will be whatever the next output was the previous time. In fact, shows that it does produce 2 31 – 1 values before cycling. One obvious limitation of the LCG used here is that it couldn’t possibly produce more than 2 31 – 1 values before repeating itself. The entire state of the LCG is a single number, whereas the Mersenne Twister maintains an internal state of 312 numbers.
#Random sequence generator generator
For example, code using the LCG generator above would be easier to debug than code using the Mersenne Twister. Some applications, such as high dimensional integration and cryptography, require more sophisticated generators, but sometimes its convenient and sufficient to use something simple.

Simple random number generators are adequate for many uses. Print( "Number of 1's: ".format(expected - 2*sd, expected + 2*sd) )Īgain the results are nothing unusual: Run length: 19 We can quantify “about” as within two standard deviations. First, we count the number of 1’s in our string of bits. # Format to print bits, padding with 0's on the left if needed Next we form a long string of 0’s and 1’s using our generator # Number of random numbers to generate # Linear congruence generator (LCG) constants We’ll need a couple math functions: from math import sqrt, logĪnd we need to define the constants for our generator. The multiplier constant was chosen to be one of the multipliers recommended in. The linear congruential generator used here starts with an arbitrary seed, then at each step produces a new number by multiplying the previous number by a constant and taking the remainder by 2 31 – 1. This post will implement a couple of the simplest tests in Python and show that the generator does well. This says more about the NIST test suite than it says about the LCG being tested. But to my surprise, the generator passed nearly all the tests, even though some more sophisticated generators failed some of the same tests. I wanted an example of a random number generator where the tests failed, and so I used a simple generator, a linear congruence generator.
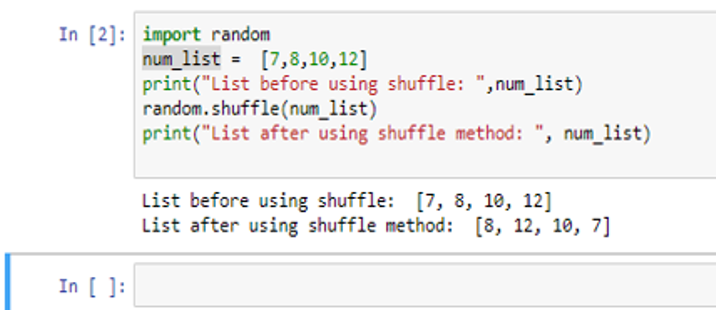
I was running the NIST statistical test suite recently.


 0 kommentar(er)
0 kommentar(er)
